relativity

relativity revision notes

revision notes from the third-year course I'm taking in general relativity, intended for future students

note that herein we work in ; all occurrences of a time variable \(t\) are implicitly a coefficient of \(c\).

week 0 (some prerequisites that i impose :-)

it will be useful later to reference s.

with a constant \(j\) satisfying \(j^2=1\), we get an analogue of complex numbers with properties:

the norm \(\Vert z\Vert\) (satisfying \(\Vert z_0z_1\Vert=\Vert z_0\Vert\Vert z_0\Vert\)) is instead \(\mathrm{Re}(z)^2-\mathrm{Jm}(z)^2\); this causes the unit numbers (that form a group under multiplication) to form a unit hyperbola (of points \((\cosh(x),\sinh(x))\)) instead of circle.
multiplication by a complex number acts as a rotation and scaling (due to the ), so all analytic functions of the complex plane are conformal maps to itself; meanwhile, by a split-complex number acts as a diagonal shear and scaling. (See Will Bolden's domain colourer, which lets you render functions' continuations into both complex planes; interestingly, trigonometric functions become periodic in both axes!)
the norm can be negative, and the set of points along diagonals have zero norm, and \((1+j)(1-j)=1+0j-j^2=0\); the existence of zero divisors downgrades their status from a field to a ring. This means that defining \(k=\frac{1+j}{\sqrt2}\) and \(l=\frac{1+j}{\sqrt2}\) (two numbers which square to themselves), we have\[(x_0k+y_0l)(x_1k+y_1l)=x_0x_1k+y_0y_1l\]so by decomposing into the \(k,l\) basis, we find that the set of split-complexes is \(\cong\mathbb R^2\)

week 1 (special relativity)

in Newtonian physics, one cannot measure their own velocity with respect to some absolute reference frame, since interactions depend only on their interactants' velocities relative to each other.(ie. isotropic => invariant under rotation, homogeneous => invariant under translation, "velocitogeneous" => invariant under velocity-change)

however, Maxwell's equations state the speed of light is constant.

the idea that light is constant in a basis reference frame called the æther was called into questionby the

the Earth's movement within this basis frame would affect the distance the light travels.

say Earth is moving at \(v\) in the \(x\) axis, and you shine a ray moving at \(c\) 1m to and from a mirror in the \(x\) axis; it takes \(\frac{1m}{c-v}\) to get there, and \(\frac{1m}{c+v}\) to get back, so \(\frac2{c-\frac{v^2}c}\) time in total.

meanwhile, firing it perpendicular to \(x\) (from the Earth's frame) means the light travels (in the basis frame) with a hypotenuse speed of \(c\) but an \(x\)ward component of \(v\), so (in the Earth frame) moves with speed \(\sqrt{c^2-v^c}\).

since \(\frac{2m}{c-\frac{v^2}c}>\frac{2m}{\sqrt{c^2-v^2}}\) (for \(0\lt v\lt c\)), travelling with the Earth would be slower than perpendicular, which could be observed via phase-shift (but was not)

there was an æther drag hypothesis that the earth would be affecting the velocity of æther it moves through, like a shockwave

however Einstein observed that other parts of Maxwell's equations, like moving a magnet through a conductor, were velocitogeneous, so wanted an ætherless theory in which light can be too

that is, every inertial reference frame observes the same laws of physics

however, whereas Newton's physics is invariant under translation, rotation and of inertial frame (multiplying spacetime positions \(\begin{pmatrix}\vec s\\t\end{pmatrix}\) by \(\begin{pmatrix}1&-\vec v\\0&1\end{pmatrix}\)), Einstein's special relativity would replace those with Lorentz boosts (multiplying by \(\begin{pmatrix}\cosh(\zeta)&-\sinh(\zeta)\\-\sinh(\zeta)&\cosh(\zeta)\end{pmatrix}\), where \(\zeta\) is the 'rapidity' of the boost)

this is for special relativity in 1+1D (in which case it is equivalent to multiplying the position vector by a split-complex 'unit number,' when considering time the reals and space the jmaginaries); now the full 3D case

(in Planck units) if a frame \(F'\) is moving at speed \(\vec v\) relative to frame \(F\), the Lorentz factor (number of seconds perceived by an observer moving with \(F'\) for what one in \(F\) measures as 1 second) is \(\gamma=\frac1{\sqrt{1-v^2}}\); with \(\alpha=\frac{\gamma^2}{1+\gamma}\), transforming from \(F\) to \(F'\) is done by

\[\begin{pmatrix}x'\\y'\\z'\\t'\end{pmatrix}=\begin{pmatrix}1+\alpha v_x^2&\alpha v_xv_y&\alpha v_xv_z&-\gamma v_x\\\alpha v_xv_y&1+\alpha v_y^2&\alpha v_yv_z&-\gamma v_y\\\alpha v_xv_z&\alpha v_yv_z&1+\alpha v_z^2&-\gamma v_z\\-\gamma v_x&-\gamma v_y&-\gamma v_z&\gamma\end{pmatrix}\begin{pmatrix}x\\y\\z\\t\end{pmatrix}\]

with \(u=\frac v{\Vert v\Vert}\) and \(\beta=\Vert v\Vert^2\alpha=\gamma-1\), this becomes

\[\begin{pmatrix}x'\\y'\\z'\\t'\end{pmatrix}=\begin{pmatrix}1+\beta u_x^2&\beta u_xu_y&\beta u_xu_z&-\gamma\Vert v\Vert u_x\\\beta u_xu_y&1+\beta u_y^2&\beta u_yu_z&-\gamma\Vert v\Vert u_y\\\beta u_xu_z&\beta u_yu_z&1+\beta u_z^2&-\gamma\Vert v\Vert u_z\\-\gamma\Vert v\Vert u_x&-\gamma\Vert v\Vert u_y&-\gamma\Vert v\Vert u_z&\gamma\end{pmatrix}\begin{pmatrix}x\\y\\z\\t\end{pmatrix}\]

the determinant of the \(3\times3\) space-to-space submatrix is again \(1+\beta(u_x^2+u_y^2+u_z^2=1)=\gamma\), and of the total is \(1\) (ie. the compression of both time and space is counteracted by the amount they add to each other).

we get out the rapidity formulation by using \(\gamma=\cosh(\zeta),\gamma\Vert v\Vert=\sinh(\zeta)\); the benefit of this is that composing two boosts in the same direction adds their hyperbolic angles.

note that in the 1+1D case, the eigenvalues are diagonal (and 'lightlike'); if \(F'\) is moving in positive \(x\) from \(F\)'s perspective with rapidity \(\zeta\), then within \(F'\), light travelling in positive \(x\) is \(e^\zeta\) times denser in spacetime, and in negative \(x\) is \(e^\zeta\) times sparser (the two eigenvectors being lightlike); in the \(n+1\)D case, there are two perpendicular eigenvectors with distinct eigenvalues (compression and dilation), and the rest of the dimensions in a trivial eigenspace with eigenvalue \(1\)

as one 'zooms in' and \(\Vert v\Vert\rightarrow0\), Lorentz transformations approach Galilean transformations, and the perception of special relativity approaches classical physics

on p. 27 of the slide, the Michelson-Morley experiment is again described, except in this case (since measurement in the same earthly reference frame would give a constant speed) as measured by an observer in an "æther frame" as the Earth moves past at speed \(v\).

so, in the Earth's reference frame, the light moves from \(\begin{pmatrix}x\\y\\t\end{pmatrix}=\begin{pmatrix}0\\0\\0\end{pmatrix}\) to \(\begin{pmatrix}1\\0\\1\end{pmatrix}\) (we need not distinguish \(y\) and \(z\) here)

\[\begin{pmatrix}x'\\y'\\t'\end{pmatrix}=\begin{pmatrix}1+\beta u_x^2&\beta u_xu_y&-\gamma\Vert v\Vert u_x\\\beta u_xu_y&1+\beta u_y^2&-\gamma\Vert v\Vert u_y\\-\gamma\Vert v\Vert u_x&-\gamma\Vert v\Vert u_y&\gamma\end{pmatrix}\begin{pmatrix}1\\0\\1\end{pmatrix}=\begin{pmatrix}1-\gamma\Vert v\Vert u_x+\beta u_x^2\\u_y(\beta u_x-\gamma\Vert v\Vert)\\\gamma(1-\Vert v\Vert u_x)\end{pmatrix}\]

if the observer moves perpendicular to the light (\(u_x=0,u_y=1\)), it will observe the light travelling in \(\begin{pmatrix}1\\-\gamma\Vert v\Vert\\\gamma\end{pmatrix}=\begin{pmatrix}1\\-\sinh(\zeta)\\\cosh(\zeta)\end{pmatrix}\)
if the observer moves parallel (\(u_x=\pm1,u_y=0\)), it will observe \(\begin{pmatrix}1\mp\gamma\Vert v\Vert+\beta\\0\\\gamma(1\mp\Vert v\Vert)\end{pmatrix}=\begin{pmatrix}\cosh(\zeta)\mp\sinh(\zeta)\\0\\\cosh(\zeta)\mp\sinh(\zeta)\Vert\end{pmatrix}\), as aforementioned

so, we have the table of observed times

	parallel	perpendicular
classical	\(\frac{2m}{1-v^2}\)	\(\frac{2m}{\sqrt{1-v^2}}\)
relativistic	\(\frac{2m}{\sqrt{1-v^2}}\)	\(\frac{2m}{\sqrt{1-v^2}}\)

the equivalence follows from velocitogeneity; the time taken by the light to do the closed loop is constant from the reference frame of the emitter/detector in \(F\) irrespective of the light's direction, and remains so when time-dilated by a Lorentz boost.

similarly to how the orbits under trigonometric rotations are circles of constant \(\mathrm{Re}^2+\mathrm{Im}^2\), the orbits under hyperbolic ones are hyperbolae of constant \(\mathrm{Re}^2-\mathrm{Jm}^2\); since a 3+1D hyperbolic rotation has time form \(\mathrm{Re}\), one space vector form \(\mathrm{Jm}\), and the spatial plane perpendicular to both left invariant, the orbits under the union of all rotations are hyperboloids.

each spacetime hyperboloid with \(s=\mathrm{sgn}(t)\sqrt{t^2-x^2-y^2-z^2}\) has the physical interpretation as being the set of points that the origin (travelling with any constant velocity) will take a constant amount of time (in its own inertial reference frame) to reach; if point \(B\) in spacetime has a given value of \(s\) from \(A\)'s reference frame, \(A\) will have a value of \(-s\) from \(B\)'s.

two sheets	cone	one sheet

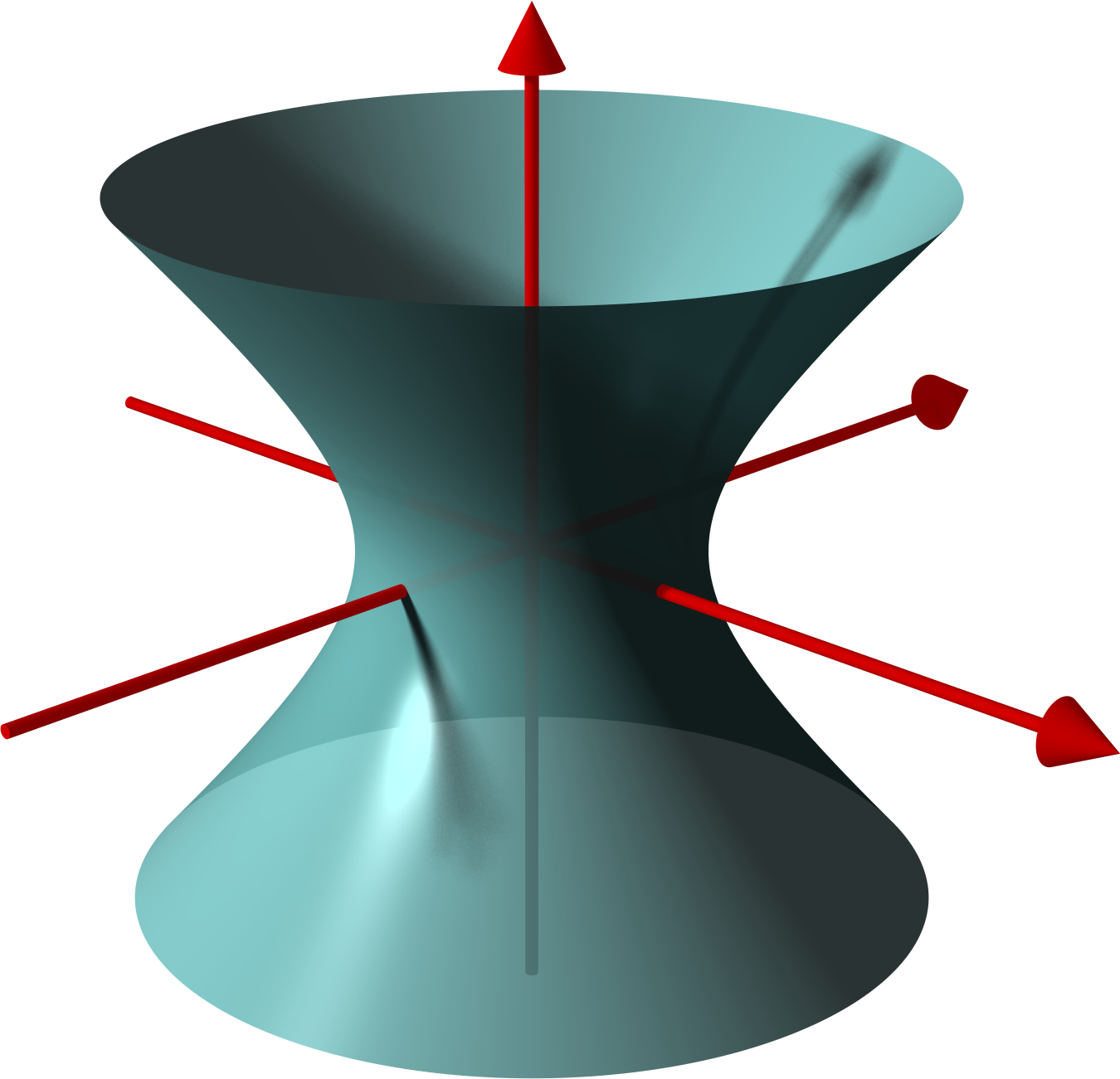
note that as wll as hyperboloids inside the cone (of points a constant perceptual time away from you irrespective of trajectory) and the cone (of points you could reach at lightspeed), there are also hyperboloids outsiede the cone (of points you are accursed never to access or vice versa)

we can also adjust the aforementioned relativistic Michelson-Morley experiment; say instead an emitter in frame \(F\) fires off two photons \(\Delta t\) time apart, which are received by another in frame \(F'\); Newtonianly, their distance in space from the observer's reference frame is \(\Delta x'=(1-v\cos(\theta))\Delta t\) (with \(\theta\) the angle between the observer's direction to emitter and direction of motion), and Einsteinianly, their distance in \(F'\) time is thus \(\Delta t'=\frac{1-v\cos(\theta)}{\sqrt{1-v^2}}\Delta t\). (In the case that the observer is moving directly towards the emitter, this is \frac{\sqrt{1-v}}{\sqrt{1+v}}, and if moving away, \frac{\sqrt{1+v}}{\sqrt{1-v}}.)

relativity vector notation

we use superscripts to extract components of vectors, and write a change of basis as \(\vec x^\overline\alpha=(\Lambda_\beta\vec x^\beta)^\overline\alpha=\Lambda_\beta^\overline\alpha\vec x^\beta\) (using Einstein sum notation, where a letter appearing multiple times means it is being summed over; unless it's Latin, in which case it sums only over space and not time (which is given index \(0\))); the change of basis is done by the overline on the indexing to represent that the vector \(\vec x\) remains unchanged.
generally if something is subscripted, it is a tuples of vectors, so the result can be superscripted to get out a variable; in particular \(\vec e_i\) (which would more consistently be written \(\vec{e_i}\)) is the \(i\)th basis vector in a basis \(\mathcal O\); seen in \(\mathcal O\), its \(i\)th component is \(1\) and all others \(0\), so we write \(\vec A=\vec e_\alpha A^\alpha\) (but if the reference frame were \(\overline{\mathcal O}\) it would be \(\vec A=\vec e_\overline\alpha A^\overline\alpha\)).
we can also interchange order of sub- and superscript indexing; when subscripting these tuples of vectors without superscripting, the result is a covector. \(\Lambda^\overline\alpha\vec e_\overline\alpha=\vec e\), so \(\Lambda^\overline\alpha_\alpha\vec e_\overline\alpha=\vec e_\alpha\) tells us how to do changes of basis in Einstein notation
concretely, if \(\overline{\mathcal O}\) is moving at speed \(\vec v\) relative to \(\mathcal O\), then the aforementioned change-of-basis matrix's term in the \(\alpha\)th column and \(\beta\)th row is \(\Lambda_\alpha^\overline\beta\) (sometimes written \(\Lambda_\alpha^\overline\beta(\vec v)\) to emphasise that it's a function of velocity).
one should read \(\Lambda_\alpha^\beta(\vec v)\) as "the change-of-reference-frame from \(\alpha\) (stationary) to \(\beta\) (moving with \(\vec v\)"; \(\Lambda_\beta^\gamma(-\vec v)\Lambda_\alpha^\beta(\vec v)\vec x^\alpha=\vec x^\gamma\)

other facts not covered explicitly in the course

the group formed by Lorentz boosts and spatial rotations under composition is quite interesting!
note that Lorentz boosts alone do not form a group, since two non-parallel ones compose to a boost with a spatial rotation
however, if you quotient by spatial rotations, you lose grouphood (since two actions now compose to an infinite set of possible actions), but retain a distance metric
specifically, that of a hyperbolic space, like the one HyperRogue is played in!
moving in HR is equivalent to performing a Lorentz boost, and if you move the camera in a clockwise loop, your reference frame will be rotated anticlockwise: that is to say, you have angular defect, whereas in spherical space you have angular excess (as you are familiar with if you've played any space games and rotated your facing direction in a clockwise loop with pitch and yaw and found your roll shifted} clockwise)
see